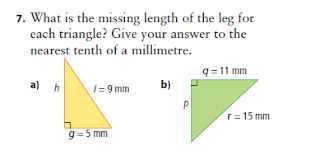
 a) Maria walked 420m.
a) Maria walked 420m. 
This is a place for the community of learners in Room 8-16 to learn and enjoy math. It is an extension of the classroom making it accessible 24 hours a day, 7 days a week.
 a) Maria walked 420m.
a) Maria walked 420m. 



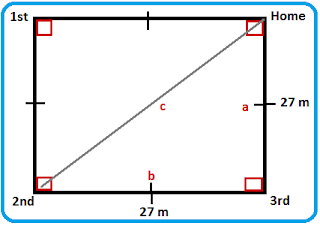
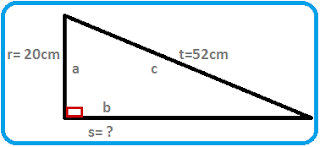
 p² + q² = r² 12m² + 35m² = r² (12² x 12² ) + (35² + 35²) = r²
p² + q² = r² 12m² + 35m² = r² (12² x 12² ) + (35² + 35²) = r²

 A triangle is made up of two smaller congruent right triangles.
A triangle is made up of two smaller congruent right triangles.




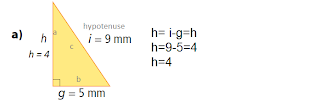

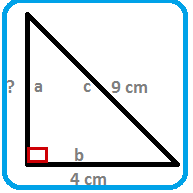


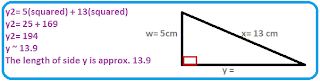
Stella is planning an outdoor wedding. She would like a square dance floor with an area of 115 m2.
a) Determine the side length of the dance floor, to the nearest tenth of a metre.
b) Stella finds out that the dance floor will be made up of floorboards that each measure 1 m2. What are the two side lengths the dance floor can have that are closest to what she wants?
c) What are the two square areas for the dance floor that Stella can choose from?
d) Which area will Stella choose? Explain.
Answers !
a.)10.7m b.) Sorry i dont know this question c.)100m2 or 121m2 d.) She will chose the 121m2 dance floor because its closer to the size she wanted.
New Question !
14. Alex is thinking of a number.
a) What number could he be thinking of?
b) Is there more than one answer? Explain
Answers!
a.) 60 b.) No, there is only one answer and the nember must be between 49 and 64. The only multiple number is 12m this is the range of 60.
